
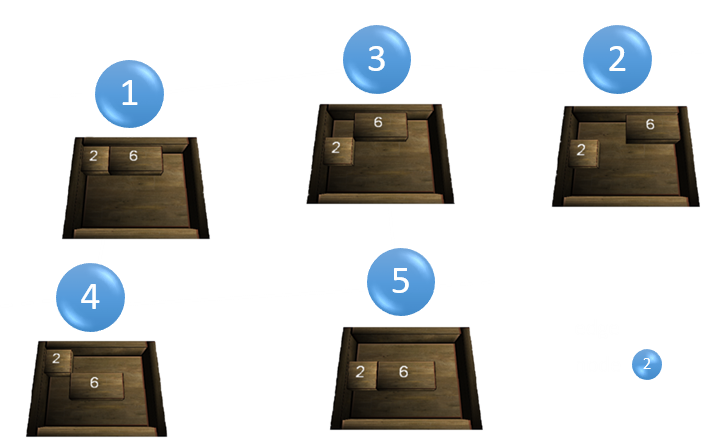
The objective of the sliding puzzle shown in this picture is to move the big 2x2-part to the bottom.
A sliding puzzle, sliding block puzzle, or sliding tile puzzle challenges a player to slide usually flat pieces along certain routes (usually on a board) to establish a certain end-configuration.
The fifteen puzzle is the oldest type of sliding block puzzle. Unlike other tour puzzles, a sliding block puzzle prohibits lifting any piece off the board. This property separates sliding puzzles
from rearrangement puzzles. Hence finding moves, and the paths opened up by each move, within the two-dimensional confines of the board, are important parts of solving sliding block puzzles.
(cited from Wikipedia)

The objective of the sliding puzzle shown in this picture is to move the big 2x2-part to the bottom.
The solving algorithm presented here is based on the in the graph theory very well known algorithm of
Dijkstra.
In mathematics and computer science a graph consists of a certain number of nodes and a collection of edges that connects pairs of nodes.
Each node as well as the edges might have a single value or a whole set of properties. In our case each node represents a unique state of
the puzzle, while the edges indicate that both connected states can be reached each other by just moving one stone for the distance of one field.
The puzzle shown in the picture above has 65880 unique states. Unique is meant here in the sence that the two situations, where for example stone 9 and 10 are exchanged, are not distinguished.
Now, finding a solution is done by performing the following three steps:
• Find all unique states and put them into a list of nodes
• Find all connected states and put them into a list of edges
• Find the shortest path between the initial and final state using Dijkstra's algorithm
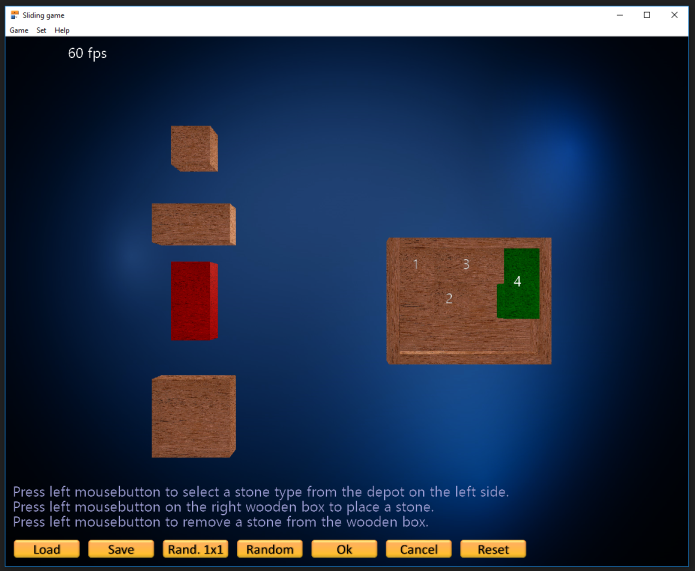
The following picture shows the dialog where the initial and target states can be defined.
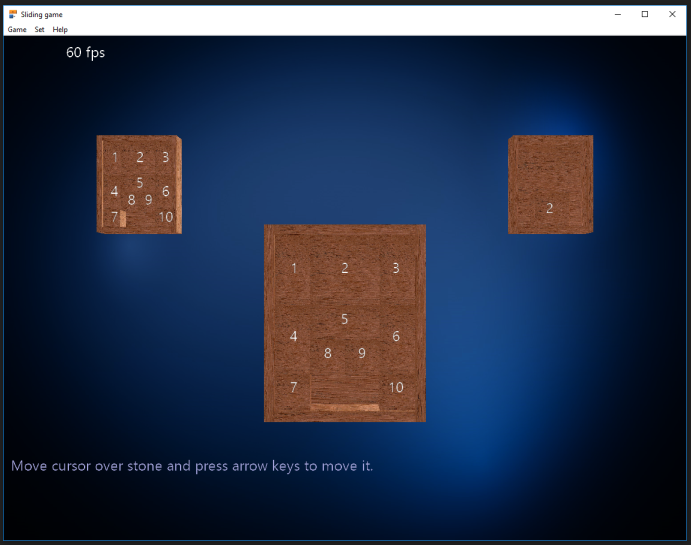
The sliding puzzle can be solved manually or ...
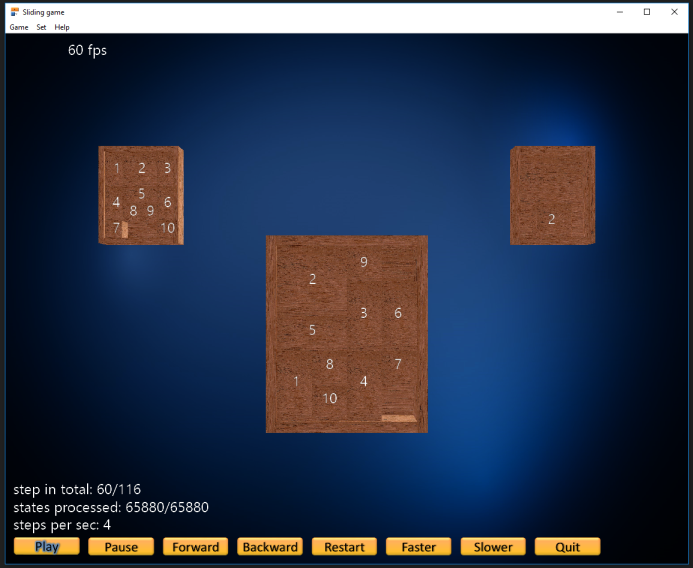
... automatically using the described algorithm above.
Exe-file, common puzzles and database:
SlidingGame_Executable_ver1.0.zip (Version 1.0, 1. Jan 2019, Win10, DirectX 11)
Sourcecode:
GitHub repositories Traga 2 and weaselLibrary
Documentation:
Solving the Sliding Puzzle Game.pdf (1. Dez 2009)