Nine Men's Morris Game - The perfect playing computer

Game description:

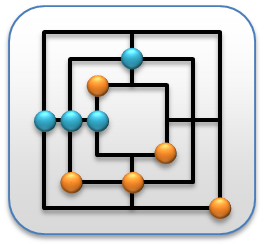
The game is played by two players and includes nine white stones, nine black stones and the game board (see Figure below) with 24 fields. The gameplay consists of three phases and will be played through in the following order: setting phase, moving phase and jumping phase. During the setting phase each player places in turn one of his nine stones on a free field. The moving phase is characterized, as the name suggests, by alternately pulling the stones along the marked lines, which each connects two fields. The final jumping phase is initiated by the player who is in possession of only three stones, who are allowed to therefore jump with his stones on each free field. A so-called mill will be closed by the arrangement of three stones of a player in a row. This can be the case in any of the three phases of the game and has the immediate removal of any opponent's stone as consequence, provided it is not part of a closed mill.

Principle of the perfect playing computer:

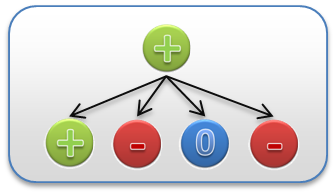
The principle of the perfect playing Nine Men’s Morris game computer is based on a database that contains information about any game situation. Each game situation is from the perspective of the player who is currently in turn. The stored information for each game situation consists of 'state value' and the minimum number of moves to win or the maximum number of moves until the game is lost, called 'ply value'. The ply value is a natural number and the state value may be in one of the following four values:

+,	if winning is possible, regardless of the actions of the enemy,
0,	if the outcome of the game is a draw,
-,	if the opponent can win with perfect play,
x,	if the situation has not yet been calculated or is invalid.

How can we derive the perfect move according to this information? Suppose an arbitrary game situation with a state value of '+'. The figure below shows four possible moves for this situation and the situation value after each of these four features. Here it is apparent that the second or the fourth move should be aspired, since they lead to game situations which seem to be lost from the perspective of the opponent.



The same principle is also applicable to situations with the value '0' in order to identify the perfect turn, while it is irrelevant for situations with the value '-', which stone is moved, because the opponents is going to win anyway with perfect playing.

The graphical user interface:

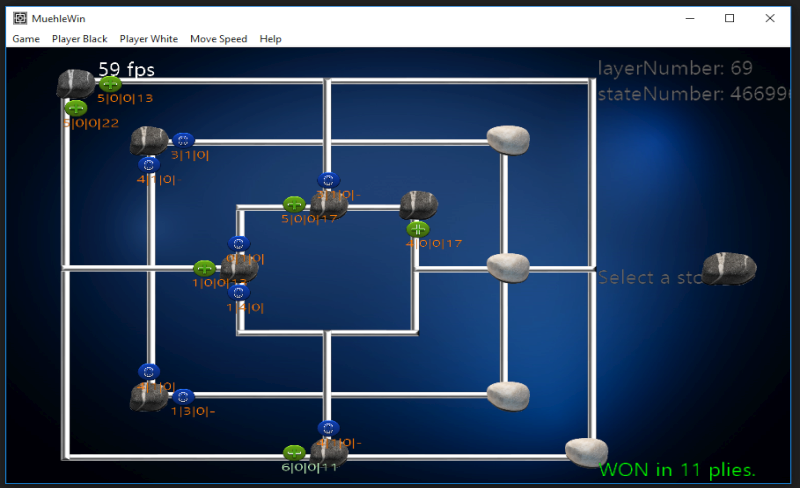
The consequence of each move is marked with one of the following three symbols and described with 4 numbers:

5 | 0 | 0 | 22		Game won in 22 moves - The next move will have 5 and no respectively . The next move will be performed by the opponent, if no mill is going to be closed.
4 | 1 | 0 | -		Drawn game - The next move will have 4 and no . Here of course no ply value can be calculated, since a drawn game lasts until forever.
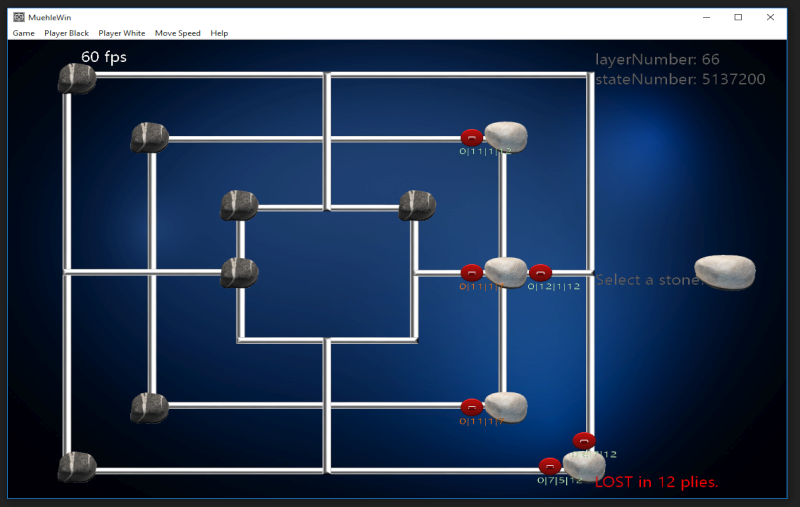
0 | 11 | 2 | 7		Lost game in 7 moves - The next move will have 11 and 2 .

In the following picture the perfect move in the preceeding image, moving the lower black stone to the left, has been performed. One can see the bad situation of the opponent player, meaning that each of his 6 possible moves are marked with a red minus. However, in order to force his opponent, you, to the maximum number of moves, he should move the white stone in the lower right corner.

Downloads:

Exe-File (Database must also be downloaded.):
MuehleWin_Executable_ver1.0.zip (Version 1.0, 1. Jan 2019, 206KB, Win10, DirectX 11)

Database (CAUTION: 8,3 GB !!!):
MuehleWin_Database_ver1.0.zip (Version 1.0, 1. Jan 2019, 8'300 MB)

Sourcecode:
GitHub repositories Muehle and weaselLibrary

Documentation:
The perfect playing Nine Men Morris computer.pdf (1. Dez 2009)